
绝对值化简是初中数学中的难点之一,本文将此类问题大致归纳为以下十种情况,进行举例分析.
一、已知不等式的解集,化简绝对值
例1 已知:x<-1,化简:∣3x+1∣-∣1-3x∣.
分析 要去掉题中绝对值,明确3x+1,1-3x的符号是关键.这里根据条件,运用不等式的性质就可以得出求出3x+1,1-3x的符号.根据不等式的性质2,由x<-1,得3x<-3.又根据不等式的性质1,得3x+1<-2,这就确定了3x+1的符号为负号.
同理,根据不等式的性质3,由x<-1,得-3x>3.又根据不等式的性质1,得1-3x>4,所以得出1-3x的符号为正号,这样就可以轻松化简.
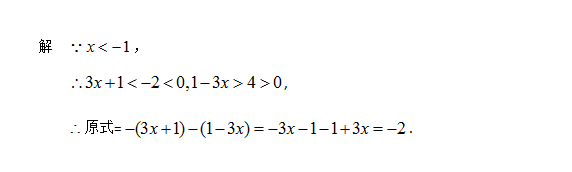
二、求出不等式的解集后,再化简绝对值
例2 已知2(1-x)<-3x,化简:∣x+2∣-∣-4-2x∣.
分析 要去掉绝对值,就得知道x+2,-4-2x的符号.要知道x+2,-4-2x的符号就得知道x地解集,要知道:地解集就要运用不等式的解法求出其解.求出x地解集后,由例1的方法就可以确定x+2,-4-2x,的符号,进而化简绝对值.
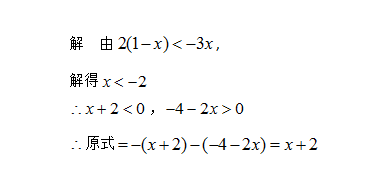
三、已知不等式的解集,化简多重绝对值
例3 已知x<-3,化简:∣3+∣2-∣1+x∣∣
分析 要去掉绝对值符号,我们只能从最里面一层一层的去掉.先根据不等式的性质,用例1的方法判断1+x的符号,去掉第一个绝对值,然后再合并同类项后判断符号,去掉第二个绝对值,最后去掉第三个绝对值.解答本题的关键是确定去绝对值符号的顺序.

四、已知不等式组的解集,化简绝对值
例4 -2<x<3,化简:∣x+2∣-∣x-3∣
分析 要去掉绝对符号,只要知道x+2,x-3的符号即可.但是与上面的例题的情况不一样,这是不等式组的解集,该如何用呢?实际上只要我们按照不等式的性质代进去一试结论就有了.根据不等式的性质1,由-2<x<3,得0<x+2<1.同样可以确定x+2的符号为正号.又根据不等式的性质,由-2<x<3,得-5<x+3<0,可以确定x-3的符号为负号.这样去绝对值符号就迎刃而解.
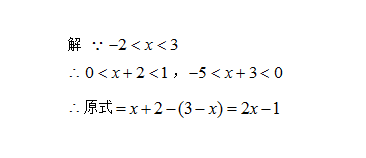
五、解答不等式组,再化简绝对值








