在我们眼里,数轴是一根再普通不过的横线,这根横线是连续的。

但真是这样吗?
数轴是由点构成的,每一个点对应一个数字。那我们仔细想一下,数字和数字无缝隙地连在一起意味着什么呢?我们肯定说不清。
这里只考虑有理数的情形。
我们知道,有理数都可以用m/n来表示,那么,两个不同的有理数之间就必然存在差值,也就是间隙,无论这个间隙多小,它一定存在。
那么,基于上述分析,数轴就不是连续的,而是点与点之间有间隔的:

图1
虽然这个间隔可以任意小,但间隔终归存在。
正是基于上述思想,数学家们定义了无穷小的概念:
无穷小比0大,但又比任何一个数字都小。
图1中的间隔不管多小,因为每个点都对应一个确定的数字,所以两个邻近点的间隔也是一个确定的数字。那么,按照无穷小的定义,它比数轴上任意两个点之间的间隔都要小,因此,无穷小可以放置在数轴上任意两个相邻的点之间:
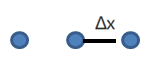
导数也正是基于这样的思想定义的:
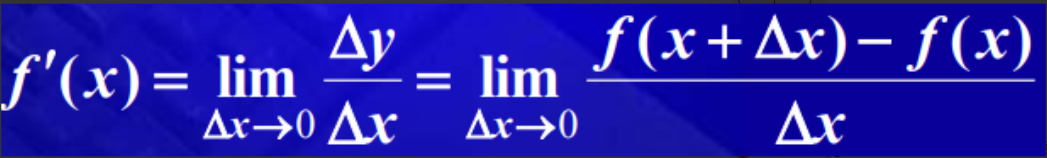
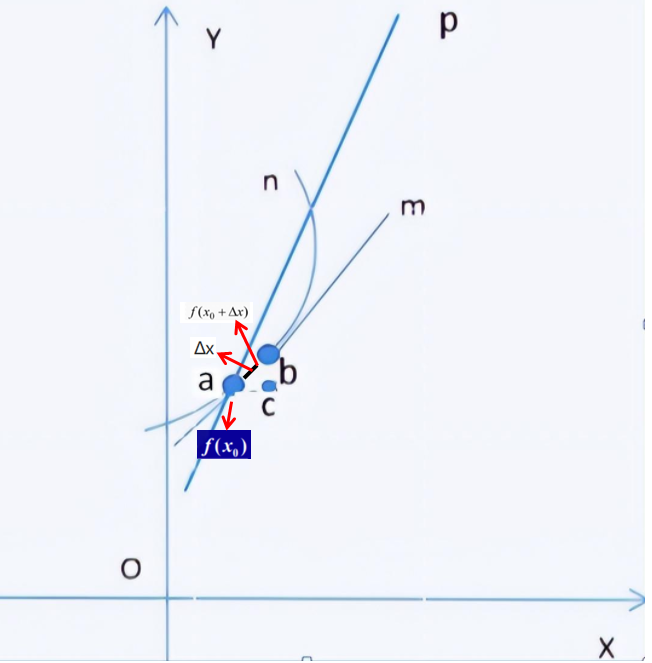
上图中,把一个无穷小线段Δx放置在任意一个与切点a相邻的点b之间,由于Δx是无穷小,我们可以认为Δx同时处于曲线n与切线m上面,从而可以精确到求出点a的导数,也就是斜率。
简单来说:
1:数学上的数轴其实不是一根连续的直线,而是由一个个分开的点构成的;
2:真是基于数轴上的点有间隔这一事实,数学家定义了无穷小的概念;
3:无穷小可以放置在数轴上任意两个相邻的点之间;
4:由无穷小进一步定义了导数、积分等概念。







